La scoperta dei numeri irrazionali è avvenuta grazie ad una setta

Fu punito con la morte per la sua scoperta dei numeri irrazionali - almeno questa è la leggenda che circonda l'antico studioso Ippaso di Metaponto. Ciò che accadde realmente nel V secolo a.C. è ancora oggi poco chiaro.

Ippaso pare appartenesse ai Pitagorici, una setta che si concentrava, tra le altre cose, sulla matematica e sul misticismo dei numeri. Un elemento centrale dei loro insegnamenti riguardava le relazioni numeriche armoniche, che includevano le frazioni di numeri interi. Dal punto di vista dell'epoca, il mondo intero poteva essere descritto utilizzando numeri naturali e razionali. Tuttavia, quando Ippaso esaminò i rapporti di lunghezza di un pentagramma - il simbolo dei pitagorici - si rese conto che alcune lunghezze dei lati non potevano essere espresse come frazioni.

Questa fu la prima volta che i pitagorici si accorsero che la lunghezza dei lati non poteva essere espressa come frazioni.

Questa fu la prima prova documentata dell'esistenza dei numeri irrazionali. Alcune storie dicono che i pitagorici si offesero per questo, perché tali numeri violavano la loro visione del mondo. In altre interpretazioni, Ippaso aveva pubblicato il suo risultato e quindi violato le disposizioni di riservatezza del patto. In ogni caso, Ippaso pare sia annegato in mare dopo la sua scoperta. A volte si dice che i pitagorici lo abbiano gettato da una nave dopo che li aveva informati della sua scoperta - oppure che la sua morte sia stata un incidente, ma i pitagorici la consideravano una punizione di Dio. Le interpretazioni correnti presuppongono che nulla di tutto ciò sia vero. Al contrario: la scoperta di Ippaso era già riconosciuta all'epoca come una scoperta matematica di cui i Pitagorici andavano fieri - a patto che la prova provenisse effettivamente da Ippaso. Perché nemmeno questo è certo.

L'unica cosa che è stata tramandata è che i pitagorici hanno dimostrato l'incommensurabilità di alcune quantità, da cui deriva l'esistenza dei numeri irrazionali. Gli stessi pitagorici sono anche oggetto di numerose storie, la cui veridicità è spesso discutibile. La comunità fu probabilmente fondata nell'attuale Italia meridionale da Pitagora di Samo - lo studioso greco da cui prende il nome il famoso teorema di Pitagora (anche se non è chiaro se abbia effettivamente dimostrato il teorema).

I Pitagorici rifiutavano la ricchezza e conducevano uno stile di vita vegetariano e ascetico. Credevano anche nella reincarnazione, il che li distingueva dal resto della popolazione greca antica. Oltre alla matematica, la comunità si occupava probabilmente di filosofia e politica. Tuttavia, le loro opinioni non erano molto popolari, motivo per cui furono perseguitati: Ci furono diversi attacchi alla comunità; alcuni decenni dopo la morte di Pitagora, la lega scomparve completamente.

Numeri oltre le frazioni

Anche se molto dei Pitagorici rimane misterioso, sono ampiamente considerati come gli scopritori dei numeri irrazionali. Oggi impariamo a scuola che esistono valori che non possono essere espressi come quoziente di due numeri interi. Tuttavia, questa consapevolezza non sembra affatto naturale: dopo tutto, tutti i valori irrazionali possono essere approssimati esattamente da frazioni - anche se è più difficile con alcuni numeri irrazionali che con altri.

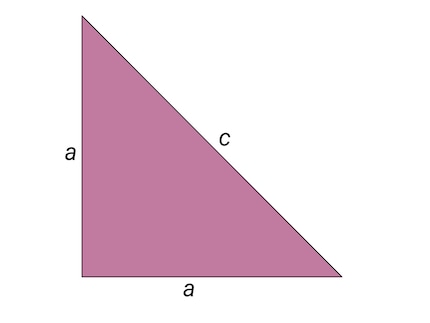
La prova presentata da Ippaso (o da un altro pitagorico) è più facilmente illustrabile con un triangolo isoscele e uno rettangolo, anche se la prova originale fu probabilmente eseguita su una figura geometrica diversa (probabilmente il pentagono). I due cateti di lunghezza a in un triangolo isoscele rettangolo formano quindi un angolo retto, di fronte al quale si trova l'ipotenusa di lunghezza c.

Un triangolo di questo tipo ha un rapporto d'aspetto fisso a⁄c. Se sia a che c sono numeri razionali, le lunghezze dei lati del triangolo possono essere scelte in modo che a e c corrispondano ai più piccoli numeri naturali possibili (cioè non abbiano divisori comuni). Ad esempio, se il rapporto d'aspetto è ⅔, sceglierai a = 2 e c = 3. Questo significa: supponendo che le lunghezze del triangolo corrispondano a numeri razionali, a e c sono numeri interi e non hanno divisori comuni.

Una prova di contraddizione

Hippasos utilizzò questo fatto per creare una contraddizione e dimostrare così che l'ipotesi iniziale doveva essere sbagliata. In primo luogo, utilizzò il teorema di Pitagora per esprimere la lunghezza dell'ipotenusa c in funzione dei due cateti a: 2a2 = c2. Poiché a e c sono numeri interi, dall'equazione precedente si deduce che c2 deve essere un numero pari. Di conseguenza, anche c è divisibile per due: c = 2n, dove n è un numero naturale.

Sostituendo c = 2n nell'equazione originale si ottiene: 2a2 = (2n)2 = 4n2. Le due equazioni possono essere ridotte da entrambi i lati, ottenendo il seguente risultato: a2 = 2n2. Poiché anche a è un numero intero, ne consegue che a2 e quindi anche a sono numeri pari. Tuttavia, questo contraddice l'ipotesi iniziale: se a e c sono entrambi pari, non possono essere divisori.

Questo ha permesso a Ippaso di concludere che il rapporto di aspetto di un triangolo rettangolo isoscele a⁄c non può corrispondere a un numero razionale. In altre parole, esistono numeri che non possono essere rappresentati come il rapporto di due valori interi. Ad esempio, se si scelgono le lunghezze dei due lati del triangolo a = 1, allora c = √2. E come sappiamo oggi, √2 è un numero irrazionale. Le sue cifre decimali continuano all'infinito senza mai ripetersi.

Dal punto di vista odierno, l'esistenza di valori irrazionali non sembra troppo sorprendente perché ci troviamo di fronte a questo fatto in età molto giovane. È difficile valutare quale effetto possa aver avuto una simile consapevolezza circa 2500 anni fa. In ogni caso, deve aver stravolto la visione del mondo matematico. Non c'è da stupirsi che ci siano così tanti miti e leggende su questa scoperta.

Spettro della scienza

Siamo partner di Spektrum der Wissenschaft e vogliamo rendere le informazioni fondate più accessibili a te. Segui Spektrum der Wissenschaft se ti piacciono gli articoli.